Population Estimate
As of June 2017, we estimate that Rocky Creek contains approximately 344 mussels, with 276 James River spinymussels and 93 Villosa Constricta (Notched Rainbow) mussels. Each species was calculated separately using the equations below.
After one hour of collecting mussels, we searched for a method of estimating the population size. We decided to tag the mussels using the Mark and Recapture method and used two equations to calculate the population. Both methods require a minimum of two days of data before an estimate can be calculated. The first day, we would go into the field to find mussels at their site. They tagged any mussel with a specific number, then placed it back into its original location. On the following days, the same method was used, however, any mussels that were already marked would be written down as a recapture and then replaced in the river. This data was used to calculate a population estimate using both methods.
Lincoln Peterson Index
The first method, the Lincoln Petersen index, is as follows:
RS =MN
Where:
R = the number of animals recaptured and released on the second day
S = the number of the captured mussels in total on the second day
M = the number of animals marked and released on the second day (newly found mussels)
N = the estimated population size.
To calculate for the population (N) the equation was rearranged:
N =(MS)/R
Unfortunately, before calculating, we found this test comes with 7 prerequisites:
-
Marked animals have the same survival rate that an unmarked animal does. Tags must not cause harm to the animal or make them more vulnerable to predators.
-
Birth and death rates should be low within the time between first capture and second capture.
-
Immigration or emigration do not occur significantly in the time between the first capture and the second capture.
-
Marked animals must mix with the population once released.
-
Marked animals must not be easier or harder to recapture.
-
Marks or tags do not come off of the animal.
-
Recapture rate is high enough to support an accurate estimate.
Since our data may have violated the 1st, 4th, 5th, 6th, and 7th prerequisites, we used the second equation called the Schnable index:
Where:
N = population estimate
Mi= number of previously marked animals at time i
Ci= number caught at time i
Ri= the number of newly marked animals at time i
Using the Schnable Index on each of our species of mussels after every tagging event has given us the possible population estimates shown above.
Schnable Index
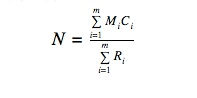
Works Cited:
"Estimating Populations Size: Mark-Recapture." TEP Lab Bench. Accessed March 30, 2016. http://www.cee.org/tep-lab-bench/pdf/PopulationSize.Worksheet.pdf